Rogue Waves: Freaks of Nature Studied with Math and Lasers
(Inside Science) -- During Columbus’ third voyage to the Americas, as his six-ship fleet sailed around the southern tip of Trinidad, an island just off the coast of Venezuela, they encountered a freak wave taller than the ship’s mast. The wave hoisted the ships up to its peak before dropping them down into a huge trough. Columbus would later name the passageway Boca del Serpiente -- Mouth of the Serpent -- for the ferocity of its waters.
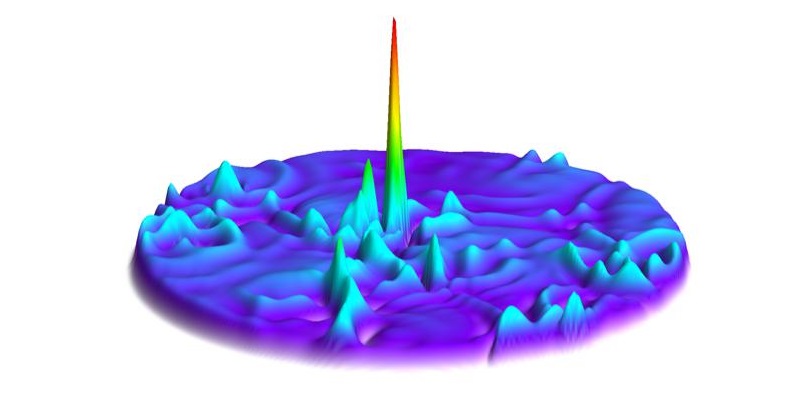
Once regarded as myths or pieces of folklore, rogue waves can spike out of nowhere and dissipate just moments later, terrifying sailors and sinking ships. Half a millennium would pass after Columbus’ encounter before the first rogue wave was measured by a scientific instrument. On New Year’s Day of 1995, the Draupner oil platform perched in the North Sea off the coast of Norway spotted a wave 84 feet tall -- more than twice the height of its neighboring waves.
Scarce data
Like stock market crashes and devastating earthquakes, the study of rogue waves has been plagued by the scarcity of data.
“The Draupner wave was the first time that a rogue wave was actually observed by a scientific instrument; before that it was all just people telling about it. But if we want to learn more about these waves, we’ll need to obtain better statistics and more data,” said Tobias Grafke, a physicist from the University of Warwick in the U.K. He is an author of a paper published in the journal Physical Review X that explored the probabilities of rogue waves from a statistical perspective.
“It's a very localized phenomenon that comes out of nowhere. I mean, you can just put certain measurement points somewhere and hope that a rogue wave would come by, but it's very, very rare,” said Hadas Frostig, a physicist from Boston University not involved in Grafke’s paper.
Moreover, “rogue waves are so strong that they often destroy the instruments trying to measure them,” said Grafke.
Due to the difficulty of collecting real-world data -- even a team of satellites would probably struggle to spot the fleeting, unpredictable waves -- researchers have mostly studied rogue waves in wave pools, dialing in specific conditions that might generate a rogue wave.
An in-lab rogue wave experiment by researchers from the University of Oxford and the University of Edinburgh. [Credit: Ton van den Bremer and Mark McAllister at the University of Oxford.]
Stacking versus interacting
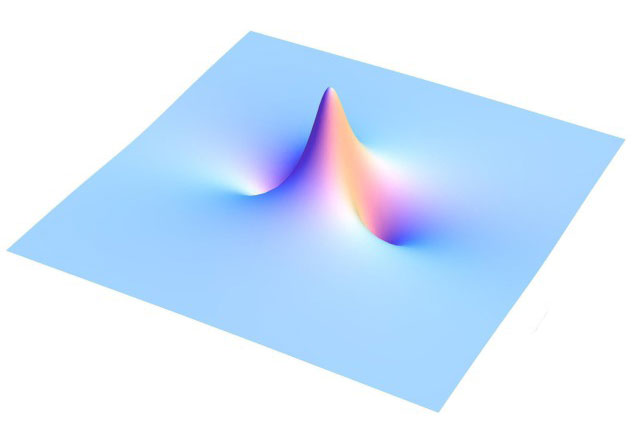
Scientists think rogue waves can be generated via two main mechanisms. In the first, waves of different wavelengths, peaking at the same spot, combine to build a massive wave. Because each of their amplitudes simply adds up to form the final height of the rogue wave, it is referred to as a linear process. In contrast, the second mechanism is nonlinear and has to do with how waves with different wavelengths interact and exchange energy with each other. (Check out this infographic by Quanta Magazine that explains the difference between the two concepts.)
A rogue wave can be built linearly or nonlinearly, or a combination of both.
Depending on how a wave model is set up, the relative importance of the two mechanisms is different. “What we want is a theory that can predict the probability of these waves and the way they evolve given the state of the ocean,” said Grafke. In other words, a model that can predict rogue waves based on the ocean condition without having to predetermine the significance for each mechanism.
Grafke and his colleagues developed a model based on mathematical concepts called solitons and instantons. Solitons are solitary excitations in a field, such as single, short pulses of light; instantons are mathematical devices for interpreting rare events in systems where random processes are present.
According to Amin Chabchoub, who studies environmental fluid mechanics at the University of Sydney in Australia and was not involved in the paper, the model is unique in its approach to predicting the occurrence of rogue waves independent of the formation mechanism.
The study of waves is rarely limited to a single medium. (For example, we have previously covered how a phenomenon called excitable waves plays a role in vastly different systems such as wildfires and heart arrhythmia.)
Since 2007, researchers have begun studying rogue waves in systems where the abundance of data is not a problem because the waves can be easily generated in huge numbers with existing technologies. Theses waves also happen to be much, much faster: light.
Then there were lasers
“Once people started studying rogue waves, it spurred this whole field where people are asking what kind of physics gives rise to these very rare, very extreme events,” said Frostig, who recently published a paper in the journal Optica that used laser systems to study rogue waves.
Using optical systems, scientists can generate the immense amount of data required to gauge the probabilities of rogue waves arising under different mechanisms. They have observed that optical rogue waves occur more frequently than would be expected if the waves’ formation were governed by Gaussian statistics, commonly known as a bell curve.
According to Frostig, rogue wave experiments in optical systems have primarily been focusing on how light waves of different wavelengths interact with each other to generate an extreme event. She and her colleagues discovered these mechanisms alone cannot account for the frequency of rogue waves present in their system. In this relatively young field, new results often create more questions than they answer.
The versatility of statistics
Optical rogue waves do not play a significant role in fiber optics systems like those that bring internet to homes and offices, because the fibers are designed to prevent signals of different frequencies interfering with each other. Nor will ocean rogue wave models likely become a practical solution for safeguarding sailors anytime soon.
But the study of rogue waves and the statistics that govern them is not limited to the ocean or fiber optics. For example, speckle patterns -- the graininess of a laser when it is projected on a surface -- is related to optical rogue waves and has applications in imaging techniques.
Rogue waves also share a mathematical framework with other systems -- some of which aren’t even waves. Protein folding, disease transmission and even some animal population estimation techniques all display similar statistical characteristics as rogue waves.
“The underlying math itself is very general, and it tells you how a system evolves around the probability of an extremely rare event, things like extreme shocks in acoustics systems, extreme voltage vortices and models for turbulence,” said Grafke. “It doesn't need to be a rogue wave.”