Math Maps the Island in Thomas More's 'Utopia'
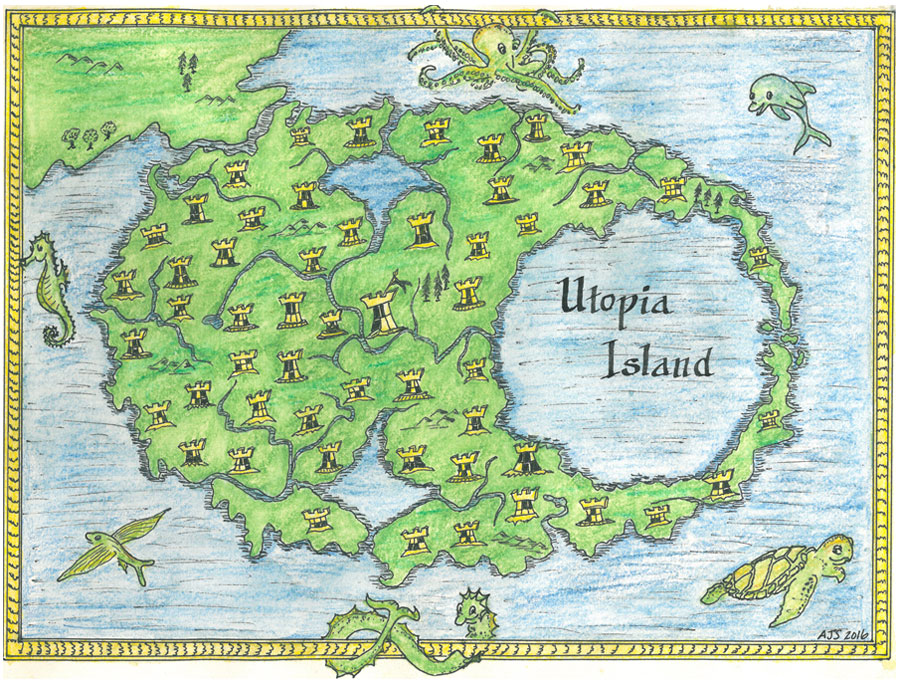
Hand-drawn map of the island of Utopia designed by Andrew Simoson
Courtesty of Andrew Simoson
(Inside Science) -- In 1516, Sir Thomas More wrote a work of fiction about a perfect society living on an island. In the text, he gave five clues for what the island would look like. Now, calculus may have revealed the true size and shape of that island, which he called Utopia.
"All of the clues are fairly clear," said Andrew Simoson, a mathematician at King University in Bristol, Tennessee.
More, an English lawyer and philosopher, wrote Utopia as a critique of England under the reign of Henry VIII. The title means "no-place" or "nowhere." Over the past 500 years, some mapmakers have puzzled over a description of the island given by the character Raphael Hythloday, who claims to have once lived there.
Hythloday explained that Utopia looked like a crescent moon with horns enclosing a circular harbor on its eastern end. There was a capital in its center, 54 city-states and a river, echoing the geography of England. He outlined other restrictions on spacing and sizes.
Over the years, several artists have attempted to construct maps of the island, but those efforts failed because they didn't satisfy some of the clues.
But by approaching it as a type of mathematical problem called optimization, Simoson believes he has designed a map that finally works.
The project began in July 2015 in Erie, Pennsylvania, when Simoson was expecting his first granddaughter's birth. While waiting, he ventured across the street to a library.
He opened up a copy of Utopia, which he had read as a college sophomore in 1972. He paged through and noticed Hythloday's description.
He thought, "Oh, wow, this is a fun mathematical problem."
Simoson looked at some illustrations on the Internet and noticed none of them fit with all the clues. Some made the river too long. Others left out cities or had the crescent horns too far apart. He decided to make his own map using calculus, a field of math for calculating area invented about 150 years after Utopia.
He translated the clues into five equations, and he decided to represent the island's coast and harbor as ellipses.
Still, a couple of Hythloday's details were ambiguous. So, to make the math work, Simoson assumed the island was symmetrical around an imaginary line that cut through the harbor's mouth and divided the island into two equal pieces. He also interpreted the location of the capital, at the center of the island, as the point you would place a pencil underneath if you were trying to balance the island on the pencil's point.
He then used a standard computer program to solve all five equations at the same time, telling him how to construct a map with the smallest possible area.
"I was somewhat surprised that the computer was able to find a solution so nicely," he said. "I wasn't quite sure the computer could handle the way I set it up."
He was able to squeeze in each city-state without breaking Hythloday's restrictions. He added two water reservoirs to sidestep a final condition about island length, and the problem was solved.
He said there are other potential models that could still satisfy all More’s conditions. The current one, however, has the smallest possible area.
He published the research in February in the magazine Math Horizons and presented the research at the annual Bridges Conference on mathematics and art in Jyväskylä, Finland, on August 10.
"It's an interesting intellectual exercise, and it's fun," said Chet Van Duzer, an independent historian of Medieval and Renaissance maps who was not involved in the research. "I don't think that's what Thomas More really wanted the reader to do or expected the reader to do."
He pointed out that the traveler's last name, Hythloday, means "peddler of nonsense" in Greek. And when Hythloday tried to give the island's location, a servant's cough blocked the words.
The math "would have fascinated More," said Anne Prescott, a Renaissance literature scholar at Barnard College in New York City who was not involved in the research. "And to say, boy, his descriptions just don't work very well, you need this kind of fancy math to make them work, yes, that's part of his joke, I think."
Andrew Silver is a contributing writer for Inside Science. He has created interactive visualizations for Quanta Magazine and written for outlets such as Science, Physics World and Live Science. Follow him on Twitter @asilver360.
Editors' note: This story has been revised to mention that the research was originally published in Math Horizons.
