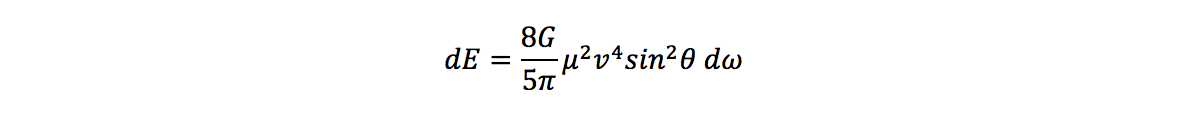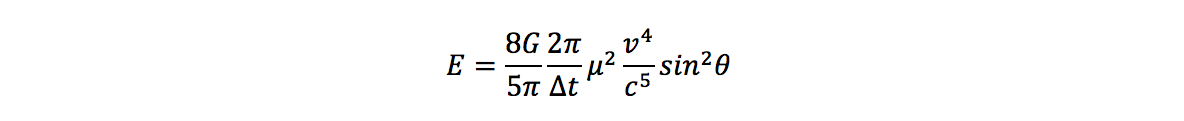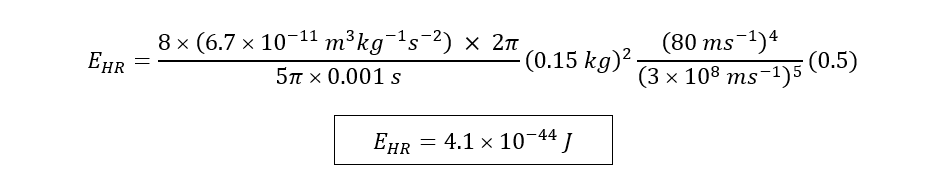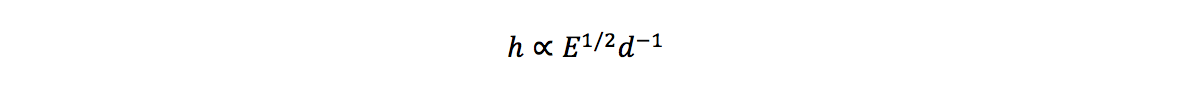Could Hitting a Home Run Produce Gravitational Waves?

Abigail Malate, Staff Illustrator
Copyright American Institute of Physics (reprinting information)
(Inside Science) -- Albert Einstein predicted a century ago that any orbiting pair of objects would make ripples in space-time and create gravitational waves. On Tuesday, a trio of researchers at Caltech and the Massachusetts Institute of Technology won the Nobel Prize in physics for finally discovering minuscule gravitational waves with the incredibly precise detectors of the Laser Interferometer Gravitational-Wave Observatory that they helped design. All four detections so far have been from pairs of black holes.
Einstein's theory of general relativity predicted that any accelerating mass has the potential to generate gravitational waves. This means that theoretically even a baseball hit off a player’s bat could produce ripples in the fabric of space-time. But how big are these ripples?
It turns out that they're really, really, really tiny.
Gravity is the weakest of forces in the universe, but pairs of giant black holes -- often tens of times more massive than the sun -- that orbit each other can emit waves, but they're only big enough to be detected if they’re not too far away. The black holes detected so far sent out waves that wobbled the detector arms by an incredibly short distance -- about one ten-thousandth of the width of a proton. LIGO, which was designed to detect these waves, has two arms that are each about 2.5 miles long. To see something smaller, you need a bigger and more sensitive detector. The European Space Agency’s Laser Interferometer Space Antenna, aiming to launch in the 2030s, will have three detectors in a triangle configuration, more than a million miles apart from each other.
A pair of neutron stars would likely give off smaller ripples, and they should be detectable by LIGO as well, but scientists haven’t reported seeing them yet. Neutron stars pack the mass of our sun into a space some 10 miles across. Since our sun is hundreds of trillions of times less dense, if we had two such stars producing gravitational waves close by, even gargantuan detectors the size of our solar system wouldn’t be big enough.
“The most important thing is the mass density,” said Jameson Rollins, a Caltech scientist and member of LIGO. “Any waves coming in the solar system, like planets orbiting around the sun or moons orbiting around planets, that’s all way, way too small.”
On Earth, even an Amtrak train passing through town or a home run ball smacked by Aaron Judge of the New York Yankees could give off the tiniest of waves. But detecting them is, it turns out, a bit impractical.
Based on an estimate worked out by Inside Science's Yuen Yiu (please see below for an extended description of the mathematical details), the energy output for the gravitational wave generated by a home run would be like dividing the energy generated by a pair of colliding black holes by the enormous number of 10 followed by 90 zeros. If you could make the LIGO detector much, much more sensitive, and set its center atop the baseball diamond, it would still have to span hundreds of times the diameter of the entire Milky Way.
While the three home runs from the Houston Astros’ Jose Altuve in yesterday’s playoff game against the Boston Red Sox might have shaken Minute Maid Park, we can’t expect those waves to ripple through the universe.
Showing Our Work: Estimating the gravitational waves of a home run
Figuring out the energy
Equation 10.4.24 from Gravitation And Cosmology: Principles and Applications of the General Theory of Relativity by Steven Weinberg describes the energy emitted in the form of gravitational radiation by a nonrelativistic two-body elastic scattering:
G is the gravitational constant 6.7×1011 m3kg-1s-2; μ = mM/(m+M) is the relative mass of the baseball bat and baseball, with M being the mass of the bat and m the baseball's; υ is the relative velocity between the ball and the bat; θ is the scattering angle between the ball and the bat.
Since in Weinberg's book he used the natural units convention, he omitted the speed of light (he assumed c = 1), we need to put 1/c5 back into the equation to find the final energy in the unit of Joules.
After integrating the right-hand side from 0 to 2π/Δt, Δt being the impact time for the hit, we end up with this:
For a home run (HR), assume the baseball flies off at a 45 degree angle such that θ =45○ and sin2θ = 0.5; assume the mass of the baseball bat much larger than mass of the baseball such that reduced mass μ = mM/(m+M) ≈ m; assume the relative velocity between the baseball and the swinging bat v is (100 + 80) mph = 180 mph ≈ 80 ms-1; assume impact time Δt = 0.001 s, then the gravitational wave energy emitted by a baseball home run, EHR, is:
If we compare this to the energy output of the first ever detected gravitational wave GW150914, estimated at EGW150914 = 3.0 M☉ × c2 = 3 × (2 × 1030 kg) × (3 × 108 ms-1)2 = 5.4 × 1047 J.
By dividing EGW150914 with EHR, the GW energy output from a home run is roughly 1.3 × 1091 times smaller than the first ever detected gravitational wave.
Figuring out the amplitude
The amplitude of the space-time strain caused by a gravitational wave is proportional to the square root of the energy source, and the inverse of the distance from source (NOT inverse-square!), such that the measurable amplitude h is as follows:
The relative amplitude of GW150914 compared with a home run hit 1 m from the detector is therefore:
Conclusion
If we naively assume that the LIGO can be linearly scaled up in sensitivity by increasing the length of the arm, i.e. the smallest detectable vibration Δl stays the same for the calculation for change over distance l, as in Δl = hl, then the required length of arm for LIGO to detect a home run from 1 meter away will scale up inversely by the ratio listed in the last equation.
Since the length for the LIGO interferometer is roughly 4000 m and its sensitivity was just enough to detect GW150914, the required LIGO's arm length if it wants to detect a gravitational wave from a home run that is only 1 m away with the same signal size as GW150914, will be:
Or more than a hundred million light years long, which is about 1,000 times the diameter of the Milky Way galaxy, longer than even the distance between us and the next 50 nearest galaxies.
(Yuen would like to thank his colleague Steve Blau for the insightful conversation that led to this exercise.)